Diagnostic TEAS Practice Exam
Take our 30 question diagnostic exam below and see how you do. It covers all subjects tested (math, reading, science, and English).
Overview of the TEAS
The TEAS exam (Test of Essential Academic Skills) is an exam given to students interested in enrolling in nursing school. The exam is administered by Assessment Technologies Institute (ATI).
The exam is used by nursing programs around the country to help schools find the best candidates for their programs.
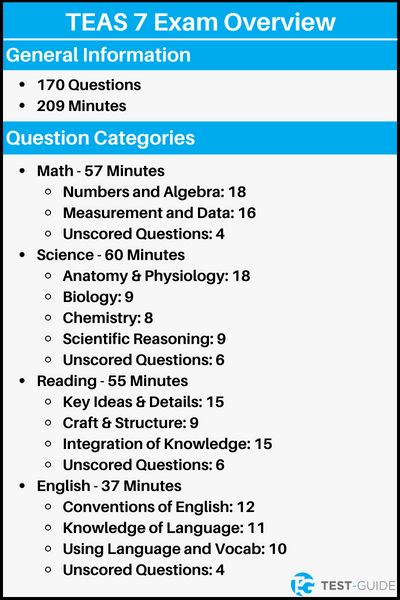
The most current version of the exam is the TEAS 7.
You can expect the following when taking the TEAS 7 exam:
- TEAS Math: 38 Questions. 57 Minutes.
- TEAS Science: 50 Questions. 60 Minutes.
- TEAS Reading: 45 Questions. 55 Minutes.
- TEAS English: 37 Questions. 37 Minutes.
Types of TEAS Questions
The TEAS exam used to be all multiple-choice questions. However, the TEAS 7 now has some different types of questions.
Some of the different types of TEAS questions you will be asked include:
- Multiple-Choice: Questions that include 4 answer choices. Only 1 answer choice will be correct.
- Multiple-Select: Questions that provide 4 or more answer choices. There may be more than 1 correct answer choice.
- Supply Answer: Questions that do not provide answer choices. You will have to fill in the blank for these questions.
- Hot Spot: Questions that provide you with an image with different “hot spots” on it. You will be asked to click the area of the image that answers the question. There are usually 2-5 “hot spots” on the image.
- Ordered Response: Questions that ask you to order a set of responses. If 1 response is out of order, the whole question is incorrect.
Take a free practice test above to prepare for these different types of questions. If you want another exam to use, you can use a TEAS practice test from BoostPrep.com.
Scoring of the TEAS
You will receive a percentage score for each of the following:
- Total Score
- Reading Score
- Math Score
- Science Score
- English and Language Usage Score
Questions on the exam are worth different values. A process called equating is used to calculate the percentage scores.
Every school sets their own minimum passing score. Typically, most schools set their minimum passing score to 70% (total score).
Learn more about TEAS scores.
Registering for the TEAS and Test Dates
There are not nationally set TEAS test dates. You can take the exam year-round.
Your specific nursing program may have requirements that will affect when you take the exam (be sure to check with them).
There are two main options for taking the exam:
- In-Person: At Your Institution or a National Testing Center
- Online: At Your Home from Your Own Computer
It is a pretty straight-forward process to register and take the TEAS. You can follow these steps to register:
- Check with your school to see if they handle the registration and payment process or if they utilize ATI for that.
- If registering though ATI, visit this page.
- Choose how you want to take the exam.
- Pay the fee (typically $120).
- Check email for confirmation.
The most important thing to remember is to check with your specific school to see if they handle the registration process or not.
How to Use a TEAS Practice Test
Using a free ATI TEAS practice test is a great way to prepare for your upcoming exam. Using practice questions will help you narrow down your studies and determine which areas you need to spend more time studying.
Some things you should pay attention to when using TEAS practice are:
- Answer Explanations: Reviewing answer explanations at the end of your TEAS test practice will help you learn difficult concepts. You may also learn a more efficient way to solve a problem.
- Timing: The timing aspect is one of the more challenging aspects of this exam. If you find yourself running out of time, try to find some ways to shave off some time. You can review the answer explanations to find a quick way to solve the problem.
- Difficult Concepts or Subjects: You may find yourself consistently struggling with 1 specific subject. If this is the case, you should focus on that subject until you are comfortable.
When practicing for the TEAS, we recommend the following steps:
- Take our free diagnostic exam above to see where you stand.
- Take time to review the answer explanations to really understand which subjects you struggled with the most.
- Figure out how you will be studying for the TEAS. This could include taking more TEAS practice exams or purchasing a prep course.
- Focus on the subjects you struggled with the most.
- Keep on taking practice exams until you score well on all 4 sections of the exam.
Benefits of Using a TEAS Practice Test
Answering TEAS practice questions is one of the best ways to prepare for this exam. Some of the benefits include:
- Focused Study Time: Students can get a sense of their strengths and weaknesses when they take practice exams. Many students mistakenly spend time practicing areas that they are already strong with on and ignore their weak areas.
- Improved Timing: The TEAS 7 exam is a timed test. To achieve a high score, students must keep a steady pace. Taking a TEAS practice exam in a timed format can improve decision-making and time management for test day.
- Enhanced Problem-Solving: Tests like the TEAS assess your ability to solve problems, not just memorize information. It is critical to have strong problem-solving abilities to do well on the exam.
- Familiarity with Test Format: All standardized tests, including the TEAS, have their own unique way of presenting questions and answer choices. You will gain more familiarity and comfort with the style of the questions as you practice.
Frequently Asked Questions
What is the difference between the ATI TEAS 6 and the ATI TEAS 7 exam?
The biggest difference is the number of questions asked in each section.
ATI TEAS 6 Exam:
- Reading – 53 questions
- Math – 36 questions
- Science – 53 questions
- English – 28 Questions
ATI TEAS 7 Exam:
- Reading – 45 questions
- Math – 38 questions
- Science – 50 questions
- English – 37 questions
Are you allowed to use a calculator on the TEAS?
Yes, you are allowed to use a calculator on the TEAS exam, but you must use the calculator that the test center provides. The calculator provided will be a simple four-function calculator.
You are not allowed to bring your own calculator, nor are you allowed to use your phone, smartwatch, etc.
What is the composite score on the TEAS test?
Your score will be reported as a composite score, which is the average of your reading, math, science, and English and language usage scores. You may take the exam multiple times. If you do, your composite score will be based on your highest score in each area.
You can read more about TEAS scores for additional information.
How can I prepare for the TEAS exam?
One great way to prepare is by taking a practice test. This will help you learn more about the exam and what to expect.
After taking some practice exams, you can reevaluate where you stand. You may feel comfortable with the material, or you may feel like you need more prep.
Our #1 recommended provider is BoostPrep.
How long is the TEAS test?
The TEAS test is a total of 209 minutes. Students are given the following time limits on each section of the TEAS:
- TEAS Reading: 55 minutes
- TEAS Math: 57 minutes
- TEAS Science: 60 minutes
- TEAS English and Language Usage: 37 minutes
Should I be taking multiple TEAS practice exams?
We recommend you take at least 3 practice exams before taking your actual exam. Each practice exam serves a purpose:
- Practice exam #1 = diagnostic exam to see where you stand
- Practice exam #2 = a check to see if you are progressing throughout your studies
- Practice exam #3 = a final check to make sure you are ready for your exam

